Hydraulic calculation of pipelines: online calculator

Hydraulic calculation of pipelines allows you to calculate water flow (throughput), the length of the section, its internal cross-section and pressure drop, and compare with the recommended parameters:

Losses per 1 m of area, based on the material, are 80 - 250 Pa/m or 8 - 25 mm of water column.
The maximum water speed for internal diameters varies: 1.5 cm - 0.3 m/s, 2 cm - 0.65 m/s, 2.5 cm - 0.8 m/s, 3.2 cm - 1 m/s s, for other parameters it is limited to 1.5 m/s.
In fire-fighting pipelines, the maximum speed of water movement is 5 m/s.

Conditional permeability DN

The conditional permeability parameter DN (nominal diameter) is a dimensionless quantity; its numerical value approximately corresponds to the internal cross-section of the pipes (for example, DN 125). The numerical values of the conditional transition are selected to increase the throughput of the pipeline network within the range of 60 - 100% when moving from one conditional throughput to the next.

According to GOST 28338-89, the parameters of conditional cross-country ability (Dn in the past) are selected from the size range:

The values are selected taking into account the elimination of problems regarding the fitting of parts to each other. The nominal diameter based on the parameters of the internal section is selected based on the clear diameter of the pipe.

Nominal pressure parameter PN

The value of the nominal pressure PN (the value corresponding to the maximum pressure level of the pumped media at 20 °C) is calculated to determine the long-term operation of a pipeline network with specified parameters. The nominal pressure parameter is a dimensionless value, calibrated based on operating practice.

The nominal pressure parameter for specific pipeline systems is selected based on the actual voltage by determining the maximum value. Fittings and fittings correspond to the data obtained. To ensure normal operation of the systems, the thickness of the pipe walls is calculated based on the nominal pressure.

Results.

The obtained values of pressure loss in the pipeline, calculated using two methods, differ in our example by 15...17%! Looking at other examples, you can see that the difference sometimes reaches 50%! Moreover, the values obtained from the formulas of theoretical hydraulics are always less than the results from SNiP 2.04.02–84. I am inclined to believe that the first calculation is more accurate, and SNiP 2.04.02–84 is “safe.” Perhaps I am wrong in my conclusions. It should be noted that hydraulic calculations of pipelines are difficult to accurately mathematically model and are based mainly on dependencies obtained from experiments.

In any case, having two results, it is easier to make the right decision.

When hydraulically calculating pipelines with a difference in inlet and outlet heights, do not forget to add (or subtract) static pressure to the results. For water – a height difference of 10 meters ≈ 1 kg/cm2.

Dear readers, Your thoughts, comments and suggestions are always interesting to your colleagues and the author. Write them down below in the comments to the article!

I ask those who respect the author’s work to download the file after subscribing to article announcements!

Don't forget to confirm your subscription by clicking on the link in the letter that will be sent to you at the specified email address (may be sent to the Spam folder)!!!

Link to download the file: gidravlicheskiy-raschet-truboprovodov (xls 57.5KB).

Read an important and, I think, interesting continuation of the topic here.

Articles with similar topics

Hydraulic resistance
Calculation of a pipeline with parallel sections

Permissible parameters of excess operating pressure pe,zul

Nominal pressure parameters are used for working environments with a temperature of 20°C. As the heating level increases, the ability to withstand loads decreases, which affects the reduction in permissible excess pressure. The pe,zul indicator determines the maximum level of excess voltage allowed when the temperature increases.

Material selection

The selection of material is made based on the characteristics of the media transported through the pipeline line and the operating pressure provided for the system. It is necessary to remember about the corrosive effect of the pumped media in relation to the material of the walls of the pipeline network. Typically, pipes and chemical systems are made of steel. In the absence of high mechanical and corrosive effects, gray cast iron or unalloyed structural steel is used when developing pipes.

At high operating pressure and the absence of loads with corrosion formation, pipes made of high-quality steel or its casting technology are used. When there is a high corrosive effect or high demands are placed on the purity of products, pipes are developed from stainless steel.

To increase resistance to sea water, a copper-nickel composition is used. The use of aluminum alloys, tantalum or zirconium is allowed. Plastic compounds that are resistant to corrosive formations are widely used. They are light in weight and easy to process, which is an ideal solution for arranging sewer systems.

Hydraulic calculation of pipelines in Excel using SNiP 2.04.02-84 formulas.

This calculation determines friction losses in pipelines using empirical formulas without taking into account the coefficients of local resistance, but taking into account the resistance introduced by the joints.

On long pipelines, such as water supply and heating mains, the influence of local resistance is small compared to the roughness of the pipe walls and height differences, and often the coefficients of local resistance can be neglected in evaluation calculations.

Initial data:

d and the length of the pipeline L previously entered in the previous calculation , as well as the calculated value of the water velocity v .
1.

Select the type of pipe from the drop-down list located above cells A30...E30:

New steel and new cast iron without internals. protective coating or with bitumen protective coating, v > 1.2 m/s

Calculation results:

Based on the selected type of pipe, Excel automatically extracts the values of empirical coefficients from the database table. The database table, taken from SNiP 2.04.02–84, is located on the same “CALCULATION” worksheet.

The coefficient
m
is extracted

to cell D32: =INDEX(H31:H42,H29) =0,300

Coefficient
A 0
is extracted

to cell D33: =INDEX(I31:I42,I29) =1,000

Factor
1000 A 1
is extracted

to cell D34: =INDEX(J31:J42,J29) =21,000

A factor of
1000 A 1 /(2 g )
is extracted

to cell D35: =INDEX(K31:K42,K29) =1,070

Coefficient
C
is extracted

to cell D36: =INDEX(L31:L42,L29) =0,000

The coefficient of hydraulic resistance
i
in m.water column/m is calculated

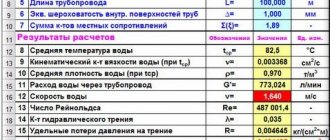
in cell D37: =D35/1000*((D33+D36/D16)^D32)/((D7/1000)^(D32+1))*D16^2 =0,057

i=((1000A1/(2g))/1000)*(((A0+C/v)m)/((d/1000)(m+1)))*v2

The calculated pressure loss in the pipeline
dP
in kg/cm2 and Pa is found accordingly

in cell D38: =D39/9.81/10000 =0,574497

dP = dP/ 9.81 / 10000

and in cell D39: =D37*9.81*1000*D8 =56358,1

dP = i * 9.81 *1000* L

Hydraulic calculation of the pipeline using the formulas of Appendix 10 SNiP 2.04.02–84 in Excel is completed!

Connection types

For the installation of individual elements of pipeline elements and fittings, fittings and apparatus, special connecting parts are used, selected based on a number of parameters:

material for the development of pipelines and fittings (the main criterion for their selection is the possibility of welding);
operating conditions: at low or high pressure, temperature conditions;
manufacturer's recommendations;
inclusion of detachable or permanent connecting parts.

Linear expansion

The geometric shape of products is changed under force or temperature. Physical stress leading to linear expansion or contraction negatively affects performance. If it is impossible to compensate for expansion, the pipes are deformed, which leads to damage to the flange seals and the areas where the pipes join each other.

When laying out pipelines, you should take into account a possible change in length with an increase in temperature or thermal linear expansion (ΔL). This parameter is determined by the length of the pipes, denoted by Lo, and the temperature difference Δϑ =ϑ2-ϑ1.

In the above formula, the coefficient of thermal linear expansion for a 1 m pipeline with increasing temperature is 1°C.

Two types of head loss

Head losses are fundamentally divided into two types:

Head loss: local (circled) and along length

Local (circled in red in the figure)
Length losses (underlined in green in the figure)

Local losses specifically in this figure: a turn, a valve (symbol according to GOST - “bow”), another turn and a sudden (i.e. not smooth) expansion.

Losses along the length here are losses in straight sections l1, l2, l3, l4.

Compensators for expansion of pipeline networks

Bends

Special bends welded into the pipeline network compensate for the natural linear expansion of products. This is facilitated by the choice of compensating U-shaped, Z-shaped and corner bends, and linear compensators.

They are designed to accommodate linear expansion of pipes due to deformation, but this technology has a number of limitations. In pipelines with increased pressure levels, elbows at different angles are used to compensate for expansion. The voltage provided in the taps enhances the corrosive effect.

Wavy expansion joints

The products are represented by thin-walled corrugated metal pipes, called bellows, which are stretched in the direction of the pipeline line. They are installed in the pipeline network, the preload serves to compensate for expansion.

The choice of axial expansion joints allows for cross-sectional expansion. Internal guide rings prevent lateral movement and internal contamination. To protect the pipes from external influences, a special lining is used. Expansion joints that do not include an internal guide ring help absorb lateral movement and vibration from pumping systems.

Insulation protection

For pipelines designed to move high-temperature media, a choice of insulation is provided:

up to 100°C, use rigid foam (polystyrene or polyurethane);
up to 600°C, the use of shaped shells or mineral fibers (stone wool or glass felt) is provided;
up to 1200°C – fibers based on ceramics or alumina.

Pipes with a conditional permeability below DN 80 and an insulating protection thickness of up to 5 s are treated with insulating shaped elements. This is facilitated by 2 shells placed around the pipes and connected using a metal tape, covered with a casing made of tin material.

Pipes with conditional flow from DN 80 are equipped with thermal insulation material with a lower frame. It includes clamping rings, spacers and metal cladding designed from galvanized mild steel material or stainless steel sheet. Insulating material is placed between the pipes and the metal casing.

The thermal insulation layer ranges in size from 5 to 25 cm. It is applied along the entire length of the pipes, on bends and elbows. It is important to exclude the presence of unprotected areas that affect the formation of heat loss. Shaped insulation serves to protect flange connections and fittings. This facilitates unhindered access to the connecting areas without removing the insulation along the entire line if the sealing properties are violated.

Length loss

Pressure loss along the length - pressure loss in pipeline sections. They arise due to the work of friction forces. (friction force occurs between layers of moving fluid). The magnitude of pressure losses, as well as local losses, directly depends on the speed of fluid movement. At a sufficiently high speed, the influence of the roughness of the pipe walls increases.

The head loss along the length can be seen by the difference in water levels between the two piezometers

Accurately determining the pressure loss along the length is a rather difficult task; for this it is necessary to establish the mode of fluid movement (sometimes laminar and turbulent), select a calculation formula for the coefficient of hydraulic friction depending on the Reynolds number Re , which characterizes the degree of turbulization of the flow. This is studied by students as part of a fluid mechanics course.

At the same time, to quickly calculate pressure losses, special tables were compiled for engineers, allowing, knowing the pipe material and its diameter, as well as water flow, to quickly determine the so-called specific pressure losses (how much pressure is lost per 1 m of pipe). This value is called 1000i, the value 1000i = 254 means that the flow passing 1 m of such a pipe loses 254 mm (millimeters) of pressure, i.e. 0.254 meters. This value is also called "hydraulic slope" and should not be confused with geodetic, i.e. simply with the physical slope (slope) of the pipe itself. To calculate steel pipes, Shevelev tables are used.

You can download the Shevelev table tables in PDF format on our website.

Reducing pressure and calculating hydraulic resistance

To determine the pressure inside the pipes and correctly select equipment that facilitates the pumping of liquid or gaseous media, it is necessary to calculate the pressure drop. In the absence of access to the Internet, calculations are made according to the formula:

Δp = λ ( l / d 1 ) ( ρ /2) v ²

Δp – voltage drops in the pipeline section, Pa l – length of the pipeline section, m λ – resistance coefficient d1 – pipe cross-section, m ρ – density level of the transported media, kg/m3 v – movement speed, m/s

Hydraulic resistance is formed under the influence of 2 main factors:

friction resistance;
local resistance.

The first option is provided for the formation of irregularities and roughness that impede the movement of the pumped media. To overcome the inhibitory effect, additional energy consumption is required. With a laminar flow and a corresponding low Reynolds index (Re), characterized by uniformity and excluding the possibility of mixing adjacent layers of liquid or gaseous media, the influence of roughness is minimal. This is explained by an increase in the parameter of the extreme viscous sublayer of the pumped media, relative to the formed irregularities and protrusions on the surface of the pipes. These conditions allow the pipes to be considered hydraulically smooth.

With an increase in the Reynolds value, the viscous sublayer has a smaller thickness, which ensures the overlap of irregularities and the effects of roughness; the level of hydraulic resistance does not depend on the Reynolds index and the average height of the protrusions on the pipe coating. A subsequent increase in the Reynolds value allows the pumped media to be transferred to a turbulent flow mode, where destruction of the viscous sublayer occurs, and the resulting friction is determined by the magnitude of the roughness.

Friction losses are calculated by substituting the data:

HT=[(λ·l)/de]·[w2/(2g)]

HT – pressure loss due to friction resistance, m
[w2/(2g)] – velocity head, m
λ – resistance coefficient
l – length of the pipeline section, m
dE – equivalent value of the cross-section of the pipeline line, m
w – speed of media movement, m/s
g – free fall acceleration, m/s2

Water pressure loss calculation

In this article we will solve the problem of pressure loss in a pipeline.
This article will help you understand how resistance to flow occurs. Using real numbers, I will describe the algorithm on how to do this. We use basic formulas. Let's look at a simple example with a pipe, as you can see in the image at the beginning of the pipe there is a pump, then there is a pressure gauge that allows you to measure the fluid pressure at the beginning of the pipe. After a certain length, a second pressure gauge is installed, which allows you to measure the pressure at the end of the pipe. Well, at the very end there is a tap. This scheme is quite simple, and I will try to give examples. So, let's begin.

In general, there is more than one way to find out the pressure loss: Method, when the pressure at the beginning and at the end of the pipe is known, you can calculate the pressure loss using the formula: M1-M2 = Pressure

, that is, this difference between the two pressure gauges. Let's say we got, roughly speaking, 0.1 MPa, which is one atmosphere. This means our pressure loss along the length is 0.1 MPa. Please note that we can indicate the loss of pressure in two quantities, this is by hydrostatic pressure, which is 0.1 MPa, and by the height of the head of the water column in meters, which is 10 meters. As I have said more than once, every 10 meters is one atmosphere of pressure.

There are a number of methods for calculating pressure loss without having pressure gauges on the pipes. Scientists have prepared wonderful formulas and figures for our use that will be useful to us.

There is a good formula that allows you to calculate the pressure loss along the length of the pipeline.

h-pressure loss here it is measured in meters. λ-coefficient of hydraulic friction is found by additional formulas, which I will describe below. L-length of the pipeline is measured in meters. D is the internal diameter of the pipe, that is, the diameter of the fluid flow. Must be inserted into the formula in meters. V is the velocity of fluid flow. Measured [Meter/second]. g-gravitational acceleration is 9.81 m/s 2

Now let's talk about the coefficient of hydraulic friction.

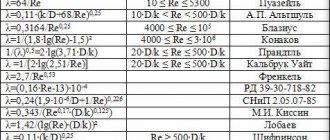
The formula for finding this coefficient depends on the Reynolds number and the equivalent pipe roughness.

Let me remind you of this formula (it only applies to round pipes):

V-Fluid flow velocity. Measured [Meter/second]. D-Inner diameter of the pipe, that is, the diameter of the fluid flow. Must be inserted into the formula in meters. ν-Kinematic viscosity. This is usually a ready-made figure for us, found in special tables.

Next, we find the formula for finding the coefficient of hydraulic friction from the table:

Here Δe

— Equivalent to pipe roughness. This value in the tables is indicated in millimeters, but when you insert it into the formula, be sure to convert it to meters. In general, do not forget to observe the proportionality of units of measurement and do not mix different types of [mm] with [m] in formulas.

d is the internal diameter of the pipe, that is, the diameter of the fluid flow.

I would also like to note that such roughness values can be absolute and relative, or even have relative coefficients. Therefore, when you look for tables with values, then this value should be called “pipe roughness equivalent” and nothing else, otherwise the result will be erroneous. Equivalent means the average roughness height.

Equivalent diameter value

Used when carrying out calculations of non-cylindrical pipeline systems (oval or rectangular cross-section). The equivalent diameter value corresponds to the parameters of a pipeline network with a circular cross-section, provided the length is the same. To carry out calculations use the formula:

d e = 4 F / P

For pipes with a cylindrical shape, the equivalent and internal cross-sections are the same. For open channels, the equivalent diameter is calculated by substituting the data:

d e = 4 F / P s

The wetted perimeter is the length of the line of interface of the transported media with the walls of the pipeline, which affects the flow restriction. Below are the perimeter shapes for different pipes.

Local resistance is formed by pipeline elements where the transported media are subject to sudden formation of deformations with a change in direction, speed or turbulence. This process can be caused by the action of valves, valves, turns and pipe forks.

Pressure loss due to local friction is calculated using the formula:

Hms=ζms·[w2/(2g)]

The level of pressure loss due to local friction is determined by the speed and coefficient of local resistance (indicated in the tabular data).

When summing up the above formulas, we obtain a general equation that allows us to determine the pump pressure:

Formulas for calculating pressure loss along length

This automated system allows you to calculate head losses along the length online . The calculation is made for a pipeline with a circular cross-section, the same diameter along the entire length, with a constant flow rate along the entire length (there are no leaks or make-up). The calculation is made for the specified liquids at a temperature of 20 degrees. C. If you want to calculate head loss at a different temperature, or for a liquid not in the list, follow the link above - I will set the kinematic viscosity and equivalent roughness myself

To get the result, you must fill out the form correctly and click the calculate button. During the calculation, the values of all quantities are converted to the SI system. If necessary, the resulting pressure loss value can be converted into pressure loss.

Procedure for calculating pressure losses

average flow velocity where Q is the fluid flow through the pipeline, A is the open cross-sectional area, A=πd 2 /4, d is the internal diameter of the pipe, m
Reynolds number - Re where V is the average fluid flow velocity, m/s, d is the diameter of the open section, m, ν is the kinematic viscosity coefficient, sq.m/s, Rg is the hydraulic radius, for a round pipe Rg=d/4, d - internal diameter of the pipe, m

The fluid flow regime is determined and a formula is selected to determine the coefficient of hydraulic friction.

For laminar flow Re
For transition mode 2000
For turbulent flow Re>4000, the universal Altschul formula. where k=Δ/d, Δ is the absolute equivalent roughness.

Pressure losses along the length of the pipeline are calculated using the Darcy-Weisbach formula.

Head and pressure losses are related.

Pressure loss along the length can be calculated using the Darcy-Weisbach formula.

Diameter of pipeline networks

When calculating the cross-section of pipes, it should be taken into account that the high speed of the pumped media reduces the material consumption of products and reduces the cost of installing systems. But an increase in speed leads to pressure losses, requiring additional energy consumption to pump media. Excessive reduction can lead to negative consequences. To calculate the optimal parameters of the cross-section of pipes, use the formula (for products with a round cross-section):

Q = ( Πd² /4) w

To calculate the optimal cross-section parameters, you need to find out the speed of the pumped media based on the summary tables:

The final equation for determining the optimal cross section is:

d = √(4 Q / Πw )

Let's look at a simple example with a pipe, as you can see in the image at the beginning of the pipe there is a pump, then there is a pressure gauge that allows you to measure the fluid pressure at the beginning of the pipe. After a certain length, a second pressure gauge is installed, which allows you to measure the pressure at the end of the pipe. Well, at the very end there is a tap. This scheme is quite simple, and I will try to give examples. So, let's begin.

There are a number of methods for calculating pressure loss without having pressure gauges on the pipes. Scientists have prepared wonderful formulas and figures for our use that will be useful to us.

There is a good formula that allows you to calculate the pressure loss along the length of the pipeline.

Next, we find the formula for finding the coefficient of hydraulic friction from the table:

Here Δe

d is the internal diameter of the pipe, that is, the diameter of the fluid flow.

In some cells of the table two formulas are indicated, you can calculate using any selected one, they almost give the same result.

In general, in general, these formulas show and prove that with an increase in speed or an increase in flow rate, the resistance to the movement of fluid flow always increases, that is, the pressure loss increases. Moreover, they increase not proportionally, but quadratically. This suggests that the unit increase in flow does not correspond to the cost of pressure loss. That is, it is not economically feasible to have a high fluid flow rate in the pipe. Therefore, it may be cheaper to increase the flow diameter. In other articles I will definitely describe how to calculate what diameter we need.

Table: (Equivalent roughness)

Who is interested in knowing ( Equivalent to roughness

) for metal-plastic, polypropylene and cross-linked polyethylene, then this corresponds and applies to
plastics
.
That is, in the table the characteristic will be: Plastic (polyethylene, vinyl plastic).
I also want to draw your attention to the fact that over time, plaque forms on the internal pipe machines, which increases the roughness of the pipes. So keep in mind that pressure loss only increases over time.

Table: ( Kinematic viscosity of water

)

Schedule:

As can be seen from the graph, as the temperature increases, the kinematic viscosity decreases, which means that the resistance to water movement decreases. This means that with a flow of hot water, the “pressure loss” will be less than with a flow of cold water. If you live in apartment buildings, if you pay attention, the speed and pressure of hot water is always higher than the pressure of cold water. There are exceptions, but in most cases this is true. Now you understand why this is so.

Now let's solve the problem:

Find the pressure loss along the length when water moves through a new cast iron pipe D=500mm at a flow rate Q=2 m3/s, pipe length L=900m, temperature t=16°C.

Given: D=500mm=0.5m Q=2 m3/s L=900m t=16°С Liquid: H2O Find: h-?

Video:

Buy the program

Solution: First, let's find the flow rate in the pipe using the formula:

V=Q/ω

Here ω

— cross-sectional area of the flow. Found by the formula:

ω=πR2=π(D2/4)=3.14*(0.52/4)=0.19625 m2

V=Q/ω=2/0.19625=10.19 m/s

Next, we find the Reynolds number using the formula:

Re=(V*D)/ν=(10.19*0.5)/0.00000116=4 392 241

ν=1.16*10-6=0.00000116. Taken from the table. For water at a temperature of 16°C.

Δe=0.25mm=0.00025m. Taken from the table for a new cast iron pipe.

Next, we check the table where we find the formula for finding the coefficient of hydraulic friction.

λ=0.11(Δe/D)0.25=0.11*(0.00025/0.5)0.25=0.01645

Next we finish with the formula:

h=λ*(L*V2)/(D*2*g)=0.01645*(900*10.192)/(0.5*2*9.81)=156.7 m.

Answer: 156.7 m = 1.567 MPa.

I also want to draw your attention to the fact that in the problem we considered a pipe that has a horizontal position along its entire length.

Let's look at an example where a pipe goes up at a certain angle.

In this case, we need to add the height (in meters) to the pressure loss to the usual problem. If the pipe goes downhill, then it is necessary to subtract the height.

We looked at the pressure loss along the length of the pipeline; there are also local resistances in the form of narrowing and turns, which also affect the pressure loss. They will be described in my other articles. And I will definitely prepare an article on how to select a pump based on pressure in order to meet the fluid flow requirements, depending on pressure losses. If something is not clear, write in the comments, I will definitely answer!

To avoid doing all the math manually, I prepared a special program:

Next article: Local hydraulic resistances

Comments
(+) [ Read / Add ]

All about the country house Water supply Training course. Automatic water supply with your own hands. For Dummies. Malfunctions of the well automatic water supply system. Water wells Well repair? Find out if you need it! Where to drill a well - outside or inside? In what cases does cleaning a well make no sense Why pumps get stuck in wells and how to prevent it Laying a pipeline from a well to a house 100% Protecting the pump from dry running Heating Training course. Do-it-yourself water heated floor. For Dummies. Warm water floor under laminate Educational Video course: According to HYDRAULIC AND THERMAL CALCULATIONS Water heating Types of heating Heating systems Heating equipment, heating batteries Heated floor system Personal article on heated floors Operating principle and operating diagram of a heated water floor Design and installation of a heated floor Do-it-yourself water heated floor Basics materials for heated water floors Installation technology of water heated floors System of heated floors Laying step and methods of laying heated floors Types of water heated floors All about coolants Antifreeze or water? Types of coolants (antifreeze for heating) Antifreeze for heating How to properly dilute antifreeze for the heating system? Detection and consequences of coolant leaks How to choose the right heating boiler Heat pump Features of a heat pump Heat pump operating principle Boiler power reserve. Is it needed? About heating radiators Methods for connecting radiators. Properties and parameters. How to calculate the number of radiator sections? Calculation of thermal power and number of radiators Types of radiators and their features Autonomous water supply Scheme of autonomous water supply Construction of a well Cleaning a well with your own hands Experience of a plumber Connecting a washing machine Useful materials Water pressure reducer Hydraulic accumulator. Operating principle, purpose and configuration. Automatic air release valve Balancing valve Bypass valve Three-way valve Three-way valve with ESBE servo drive Thermostat for radiator Manifold servo drive. Selection and connection rules. Types of water filters. How to choose a water filter for water. Reverse osmosis Sludge filter Non-return valve Safety valve Mixing unit. Principle of operation. Purpose and calculations. Calculation of the CombiMix Gidrostrelka mixing unit. Operating principle, purpose and calculations. Indirect heating storage boiler. Principle of operation. Calculation of a plate heat exchanger Recommendations for the selection of PHE when designing heat supply facilities About contamination of heat exchangers Indirect water heating water heater Magnetic filter - protection against scale Infrared heaters Radiators. Properties and types of heating devices. Types of pipes and their properties Indispensable tools for a plumber Interesting stories A scary tale about a black installer Water purification technologies How to choose a filter for water purification Let's think about sewerage Sewage treatment plants in a rural house Tips for a plumber How to evaluate the quality of your heating and plumbing system? Professional recommendations How to choose a pump for a well How to properly equip a well Water supply for the garden How to choose a water heater An example of installing equipment for a well Recommendations for the configuration and installation of submersible pumps What type of water supply accumulator should you choose? Water cycle in an apartment - vent pipe Removing air from a heating system Hydraulics and heating engineering Introduction What is hydraulic calculation? Discrepancy in hydraulic calculation Physical properties of liquids Hydrostatic pressure Let's talk about the resistance to the passage of liquid in pipes Modes of fluid movement (laminar and turbulent) Hydraulic calculation for pressure loss or how to calculate pressure loss in a pipe Local hydraulic resistance Professional calculation of pipe diameter using formulas for water supply How to choose a pump according technical parameters Professional calculation of water heating systems. Calculation of heat loss of the water circuit. Hydraulic losses in a corrugated pipe Heat engineering. Author's speech. Introduction Heat transfer processes Thermal conductivity of materials and heat loss through the wall How do we lose heat with ordinary air? Laws of thermal radiation. Radiant warmth. Laws of thermal radiation. Page 2. Heat loss through a window Factors of heat loss at home Start your own business in the field of water supply and heating systems Question on hydraulic calculations Designer of water heating Pipe diameter, flow speed and coolant flow. We calculate the diameter of the heating pipe. Calculation of heat losses through the radiator. Power of the heating radiator. Calculation of the power of radiators. Standards EN 442 and DIN 4704 Calculation of heat loss through building envelopes Find heat loss through the attic and find out the temperature in the attic Selecting a circulation pump for heating Transfer of thermal energy through pipes Calculation of hydraulic resistance in a heating system Distribution of flow and heat through pipes. Absolute schemes. Calculation of a complex associated heating system Heating calculation. Popular myth Calculation of heating of one branch along the length and KMS Calculation of heating. Selection of pump and diameters Heating calculation. Two-pipe dead-end Heating calculation. Single-pipe sequential heating calculation. Two-pipe associated Calculation of natural circulation. Gravity pressure Calculation of water hammer How much heat is generated by pipes? We are assembling a boiler room from A to Z... Heating system calculation Online calculator Calculation program Heat loss of the room Hydraulic calculation of pipelines History and capabilities of the program - introduction How to make a calculation of one branch in the program Calculation of the KMS angle of the outlet Calculation of the KMS of heating and water supply systems Pipeline branching - calculation How to calculate in the program single-pipe heating system How to calculate a two-pipe heating system in a program How to calculate radiator flow in a heating system in a program Recalculation of radiator power How to calculate a two-pipe associated heating system in a program. Tichelman loop Calculation of a hydraulic separator (hydraulic arrow) in the program Calculation of a combined circuit of heating and water supply systems Calculation of heat loss through enclosing structures Hydraulic losses in a corrugated pipe Hydraulic calculation in three-dimensional space Interface and control in the program Three laws/factors for selecting diameters and pumps Calculation of water supply with self-priming pump Calculation of diameters from the central water supply Calculation of water supply for a private house Calculation of a hydraulic arrow and collector Calculation of a hydraulic arrow with many connections Calculation of two boilers in a heating system Calculation of a single-pipe heating system Calculation of a two-pipe heating system Calculation of a Tichelman loop Calculation of a two-pipe radial distribution Calculation of a two-pipe vertical heating system Calculation of a single-pipe vertical heating system Calculation of a warm water floor and mixing units Recirculation of hot water supply Balancing adjustment of radiators Calculation of heating with natural circulation Radial distribution of a heating system Tichelman loop - two-pipe associated Hydraulic calculation of two boilers with a hydraulic arrow Heating system (not Standard) - Another piping scheme Hydraulic calculation of multi-pipe hydraulic arrows Radiator mixed system heating - passing from dead ends Thermoregulation of heating systems Pipeline branching - calculation Hydraulic calculation for pipeline branching Calculation of a pump for water supply Calculation of warm water floor contours Hydraulic calculation of heating. Single-pipe system Hydraulic heating calculation. Two-pipe dead-end Budget option for a single-pipe heating system for a private house Calculation of the throttle washer What is KMS? Calculation of a gravity heating system Designer of technical problems Extension of a pipe Requirements SNiP GOSTs Requirements for a boiler room Question for a plumber Useful links for a plumber - Plumber - ANSWERS!!! Housing and communal problems Installation work: Projects, diagrams, drawings, photos, descriptions. If you're tired of reading, you can watch a useful video collection on water supply and heating systems

Nomograms for hydraulic pipe calculations

To check pressure losses in a given area, the indicators of pressure gauges are compared with tabular data, or they are guided by the functional dependence of fluid flow on changes in voltage (at a constant diameter).

For example, a branch with 10 kW radiators is used. The fluid flow rate is calculated to transfer heat energy at a level of 10 kW. A section from the first battery in the branch was taken as the calculation section. Its diameter is constant. The second section is located between the 1st and 2nd batteries. In the second section, the energy consumption is 9 kW with a possible reduction.

The hydraulic resistance is calculated up to the return and supply pipes, this is facilitated by the formula:

G uch = (3.6*Q uch)/(c*(t rt o)),

where Q uch is the level of heat load of the area, (W). The heat load for 1 area is 10 kW;

c - (indicator of specific heat capacity for liquid) constant, equal to 4.2 kJ (kg * ° C);

tr is the temperature regime of the hot coolant;

to is the temperature regime of the cold coolant.

Hydraulic calculations of gravity heating systems: coolant transportation speed

The minimum coolant speed is 0.2-0.26 m/s. When the parameter decreases, excess air masses may be released from the liquid, leading to the formation of air pockets. This is the reason for complete or partial abandonment of the heating system. The upper threshold of coolant speed is 0.6-1.5 m/s. Failure to reach the specified speed may result in the formation of hydraulic noise. In practice, the optimal speed varies in the range of 0.4-0.7 m/s.

For more accurate calculations, the parameters of the materials for making pipes are used. For example, for steel pipes, the fluid speed varies in the range of 0.26-0.5 m/s. When using polymer or copper products, it is allowed to increase the speed to 0.26-0.7 m/s.

Calculation of resistance of gravity heating systems: pressure loss

The sum of all losses due to hydraulic friction and local resistance is determined in Pa:

Handle = R * l + ((p * v2) / 2) * E3,

where v is the speed of transported media m/s;
p—liquid density, kg/m³;
R—pressure loss, Pa/m;
l is the length used for pipe calculations, m;
E3 is the sum of all local resistance coefficients in the equipped area of the shut-off valves.

The overall level of hydraulic resistance is determined by the sum of the resistances of the design sections.

Hydrocalculation of two-pipe gravity heating systems: selection of the main branch

If the hydraulic system is characterized by associated transportation of the coolant, for two-pipe systems you should select a ring of the maximum loaded riser through the heating devices located below. For systems characterized by dead-end coolant movement, it is necessary to select a ring of the lower heating device for the most loaded of the most remote risers. For horizontal heating structures, rings are selected through the busiest branches belonging to the lower floors.

Calculator for calculating pressure loss in a water supply system

It would be wrong to assume that if, for example, a pumping station or an installed hydraulic accumulator supplies water at a certain pressure to the home pipework, then this pressure will also be at the end points of consumption. In fact, it is also necessary to lay down a certain operational reserve of the created pressure - for its inevitable losses.

Calculator for calculating pressure loss in a water supply system

The nature of these losses is different. Just to overcome the force of gravity (if, say, the pumping station or collector is located in the basement, and the consumption points are on the floors), like it or not, you have to “give up” 0.1 atmosphere (bar) for each meter of lifting height. A lot of horizontal sections are also “stolen” due to hydraulic resistance in the pipes. And the smaller the diameter and the longer the section, the more significant these losses are. Add here also turns, tees, taps and valves, filters, transitions to another diameter, etc. – each such point provides additional local resistance, reducing the overall water pressure.

And it may turn out that out of the supplied, for example, 2.5 atmospheres, only some 0.2 atmospheres reaches the distant point of water intake, and this is clearly not enough for the normal operation of the device. To avoid such incidents, it is necessary in advance, even at the design stage of your water supply system, to “model the situation”, that is, to calculate the influence of hydraulic resistance. The proposed calculator for calculating pressure losses in a water supply system can help with this.

A few necessary clarifications will be given below.

Calculator for calculating pressure loss in a water supply system

Go to calculations

Explanations for calculations

On the pages of our portal there is information on how to calculate the nominal diameter of a pipe for a water supply system, based on the required water flow and the optimal flow rate in the pipes.

How to correctly determine the diameter of a water pipe?
The main criterion is that the pipe must provide the required water flow at the end points of consumption. From here the entire further algorithm is built, implemented in the calculator for calculating the minimum required diameter of a water pipe - a link leads to the corresponding page of the portal.

But there is no need to stop there. Each of the planned “branches” of the water supply system must be analyzed from the point of view of pressure losses.

What do we indicate in the fields of the calculator?

First of all, what pressure is given at the starting point of the calculated section.

— This may be the lower setting limit of the pumping station or accumulator, that is, the pressure at which the pump turns on.

— This could be the pressure in the central collector at the point where the branch is inserted into the system.

- This could be the pressure on the collector, located on the floor, to which all the devices on this floor are then connected.

Expert opinion: Afanasyev E.V.

Chief editor of the Stroyday.ru project. Engineer.

By and large, this can generally be any arbitrary point in the system, the water pressure in which is known or calculated. For example, a small “branch” is taken from a pipe for a free-standing plumbing fixture.

That is, the entire system can be divided into a kind of “hierarchy”. For example, a pump, then risers, collectors on the floors, followed by main pipes on the floors with tie-in points, etc. That is, for each of the points you can calculate the pressure loss (using the same calculator), and then “dance” further from it.

The second point is the difference in heights between the starting and ending points of the calculated section. The indication is in meters, the program will convert it into atmospheres.
Next, sections of pipes along the path from the start to the end point are considered. Pipes with a diameter of more than 1 inch can not be taken into account - the hydraulic resistance in them is so small that it can be neglected. True, such pipes are practically never found in internal plumbing.

— When you specify the diameter that exists on the site, additional data entry fields will open.

— For each of the three diameters (½”, ¾” and 1″), you will also need to indicate the type of pipe. More precisely, are steel (including galvanized) VGP pipes used, the increased roughness of the walls of which gives much higher values of hydraulic resistance when compared with plastic, metal-plastic, copper pipes.

— The length for each diameter is the sum of the lengths of all horizontal and vertical segments in the calculated area.

If the diameter suggested in the calculator is not available on the site, then it is left as is, and it will automatically be excluded from the calculation.

Next, all the points available in the calculated area where local pressure losses are possible are indicated. More precisely, the points have already been listed for convenience - and you just need to calculate them on a drawing or plan and indicate their number. If the indicated element does not exist, you can either enter a zero, or even simply leave the line blank by default - it will automatically be excluded from the calculation.

By the way, if flexible pipes are used (for example, metal-plastic) and the turns are made without bends, only by bending, this is still taken into account. A smooth turn is simply indicated, with a radius exceeding two pipe diameters.

All that remains is to press the “CALCULATE…” button and get the predicted pressure at the far end of the calculated section. Well, compare it with what is necessary for the correct operation of the final device. Typically, a pressure of 0.5 atmospheres is sufficient for most plumbing fixtures. Less - problems may arise. In addition, some products require higher pressure levels - this is specified in their technical characteristics.

If the pressure is insufficient, you will have to somehow correct this matter. Possible methods are increasing the pressure at the starting point, increasing the diameters of individual sections, shortening the length of sections, straightening them, reducing the “saturation” of the water supply with taps, bends, etc. After each such theoretical adjustment, a control calculation is carried out. And so on until the optimal solution from all points of view is found.

Examples of nomograms

When choosing the parameters of pipes and materials for development, specialists are guided by the technological and design requirements imposed in a particular situation. To standardize dimensions, they are classified and unified, taking into account the pressure permissible for operation.